Магадлалт үндэслэл дэх Байесын сүлжээ нийтлэлийн үргэлжлэл.
Байесын сүлжээг байгуулахдаа үүсэх граф нь сийрэг, циклгүй байхын тулд системчилсэн аргачлалыг дагаж мөрддөг. Энэ DAG бүтэц нь эдгээрийн хамаарал болон үл хамаарлыг хурдан тодорхойлох боломжийг олгодог тул ашиглахад тохиромжтой.
Хувьсагчдыг тодорхойлох
Онтологит шаардлагатай хувьсагчдыг тодорхойлно. Эдгээр хувьсагч нь асуудалтай холбоотой үйл явдал, үр дүн эсвэл ажиглалтыг илэрхийлж болно. Бодит ертөнцийн олон асуудалд өндөр, масс, температур, мөнгө гэх мэт санамсаргүй хувьсагч орно. Статистикийн ихэнх нь домэйн ч мөн санамсаргүй хувьсагчтай холбоотой байдаг. Тодорхойлолтоор бол санамсаргүй хувьсагчид хязгааргүй тооны боломжит утгатай байдаг тул утга тус бүрийн нөхцөлт магадлалыг тодорхой зааж өгөх боломжгүй бөгөөд ихэнхдээ 0 гэж үздэг [4]. Санамсаргүй хувьсагчдыг зохицуулах нэгэн арга нь дискретизаци буюу боломжит утгуудыг тогтмол интервалд хуваах замаар зайлсхийх явдал юм. Жишээлбэл, температурыг < 0 цельс, 0 − 100 цельс, > 100 цельс гэж хувааж болно. Ингэж дискрет ба санамсаргүй хувьсагчтай болсон сүлжээг эрлийз Байесын сүлжээ гэж нэрлэдэг.
Оройн эрэмбийг тодорхойлох
Хувьсагчдыг логик дарааллаар байрлуулж, учир шалтгааны хамаарлыг харгалзан эрэмбэлнэ. Дүрэм ёсоор дараалалд шалтгаан нь үр дагавраас өмнө байх ёстой, учир нь энэ нь холбоосын тоог багасгаж, сүлжээг хялбаршуулдаг. Хулгайн сүлжээний хувьд хамгийн боломжит эрэмбэлэлт нь дараах байдалтай байна.
Burglary → Earthquake → Alarm → JohnCalls → MaryCalls
Энэ эрэмбэ нь шалтгааны хамаарлыг бүрэн илэрхийлэх ба зөвхөн шаардлагатай хамаарлыг зааж өгсөн. Үүссэн сүлжээ нь сийрэг бөгөөд CPT-ийн цөөн оролтыг шаарддаг. Харин доорх эрэмбэлэлт нь шаардлагыг хангахгүй. Энд MaryCalls-аас Alarm болон Alarm-аас Burglary руу чиглэсэн шаардлагагүй хамаарлыг өгч, CPT оролтын тоог нэмэгдүүлж, дүгнэлтийг төвөгтэй болгодог.
MaryCalls → JohnCalls → Alarm → Burglary → Earthquake
Хувьсагч бүрийг төлөөлөх Xi ирмэгийг нэмэх
Өмнөх 𝑋1, 𝑋2, …, 𝑋𝑖−1 хувьсагчдаас тоо нь хамгийн бага байхаар эх орой болох хувьсагчдыг тодорхойлно. Хэдийгээр эцэг оройн тоо хамгийн ихдээ k байсан ч тухайн оройн CPT-г бөглөхөд O(2k) хүртэлх боломжит нөхцлийг авч үзэх хэрэг гарах бөгөөд хамгийн муу хувилбар юм. Ийм тохиолдолд үлгэр загваруудыг ашииглаж, хэд хэдэн параметрүүдийг оруулах замаар экспоненциал тооны параметрүүдийг өгөхөөс сэргийлдэг. Эдгээр эх оройнуудаас Xi -руу чиглэсэн ирмэгийг нөхцөлт үл хамаарлын P(Xi |Xi−1, …, X1) = P(Xi |Parents(Xi)) чанарыг дагадаг байхаар графт нэмнэ.
CPT-г зааж өгөх
Хувьсагч бүрийн хувьд түүний эх оройн өгөгдсөн нөхцөлт магадлалын утгыг тодорхойлохын тулд түүний CPT-ийг тодорхойлно. Тодорхой бус хамаарлыг ихэвчлэн бохирдсон логик хамаарал гэж нэрлэдэг. Стандарт жишээ нь noisy-OR хамаарал бөгөөд энэ нь логик OR-ийн ерөнхийлөл болно. Нотолгоот логикийн хувьд ханиад, томуу, хумхаа өвчнийг үнэн гэж үзвэл халууралт үнэн гэж хэлж болно. Noisy-OR загвар нь хоёр таамаглалыг дэвшүүлдэг. Нэгдүгээрт, энэ нь бүх боломжит шалтгааныг жагсаасан гэж үздэг. Хоёрдугаарт, эцэг тус бүрийн хазаарлалт нь бусад эцгийн хазаарлалтаас ангид гэж үздэг. Доорх зургийн хувьд (a) -д хэрэв X-ийн эцгүүдийн (Ui) утгыг аль хэдийн мэдэж байгаа бол X-ийн удам бус (Zij) оройнууд нь X-тэй нөхцөлт үл хамааралтай байна. Харин (б) -д X орой нь Марковын бүрхэвчийг (саарал хэсэг) харгалзан сүлжээний бусад бүх оройноос нөхцөлт үл хамааралтай байна. Энэхүү Марковын бүрхэвчид X оройд шууд нөлөөлж буй эцэг оройнууд (Ui), X оройгоос шалтгаалж буй хүүхэд оройнууд (Yi), X оройн хүүхдүүдэд нөлөөлж буй бусад эцэг оройнууд (Zij) багтана.
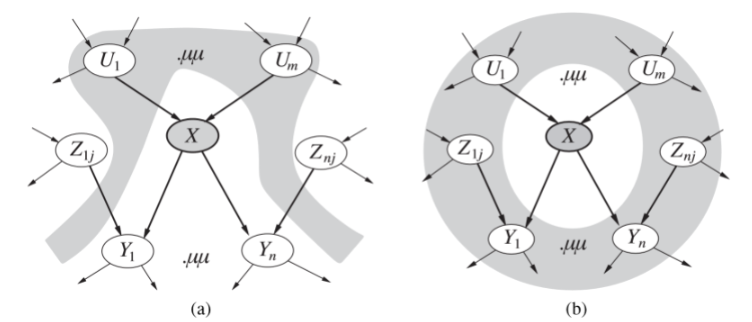
Жишээлбэл, хумхаа өвчнийг халуурахаас хазаарлаж байгаа зүйл нь ханиадны халууралтаас хазаарлах зүйлээс үл хамаарна. Эдгээр таамаглалыг харгалзан үзэхэд халуурах нь зөвхөн бүх эцэг нь хазаарласан тохиолдолд худал болох бөгөөд үүний магадлал нь эцэг эх бүрийн q хазаарлах магадлалын үржвэр юм.
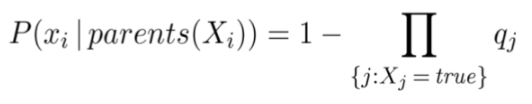
Нийт k тооны эцгээс хамаарах бохирдсон логик хамаарлыг бүрэн CPT-д O(2k)-ын оронд O(k) тооны параметрээр тодорхойлж болно. Жишээлбэл, 448 орой, 906 ирмэг бүхий CPCS сүлжээ (Pradhan et al., 1994) нь бүрэн CPT-д 133, 931, 430-ын оронд зөвхөн 8,254 утгыг шаарддаг.
Жишээлбэл, хумхаа өвчнийг халуурахаас хазаарлаж байгаа зүйл нь ханиадны халууралтаас хазаарлах зүйлээс үл хамаарна. Эдгээр таамаглалыг харгалзан үзэхэд халуурах нь зөвхөн бүх эцэг нь хазаарласан тохиолдолд худал болох бөгөөд үүний магадлал нь эцэг эх бүрийн q хазаарлах магадлалын үржвэр юм.
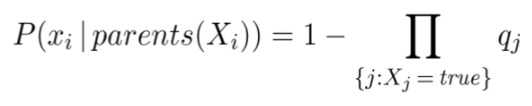
Энэ ёсоор тус бүрийн хувьд q хазаарлах магадлалыг олбол:
qcold = P(¬fever | cold, ¬flu, ¬malaria) = 0.6 ,
qflu = P(¬fever | ¬cold, flu, ¬malaria) = 0.2 ,
qmalaria = P(¬fever | ¬cold, ¬flu, malaria) = 0.1 .
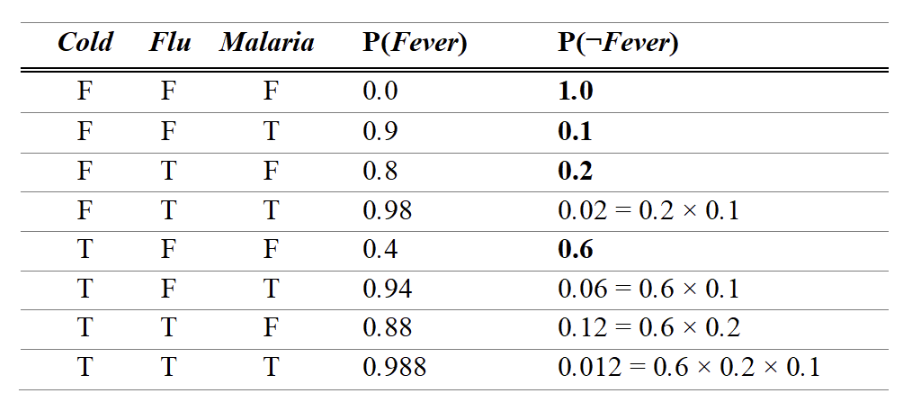
Доорх хүснэгтэд тухайн мөрөнд үнэн байх эцгүүдийн q хазаарлах магадлалын утгыг үржүүлэн авсан тооцоог үзүүлэв.
Эрлийз байесын сүлжээг тодорхойлохын тулд эцэг оройн санамсаргүй хувьсагчийн нөхцөлт тархалт болон өгөгдсөн дискрет хувьсагчийн нөхцөлт тархалтыг зааж өгөх хэрэгтэй болдог.



