Хамтдаа бодоцгооё №8

Дулмаа Анхбаяр

• 2025-08-10

“Хамтдаа бодоцгооё” цувралыг шимтэн уншдаг та бүхэнд энэ өдрийн мэндийг хүргэе. Өнөөдрийн дугаарт бид Competitive Programming чиглэлд хамгийн түгээмэл орж ирдэг асуудал болох палиндром тоо сэдвийн сонирхолтой асуудлыг шийдэхээр сонголоо.

Та анзаарсан бол бидний сонгодог бодлогууд ихэвчлэн SPOJ сайтаас авсан байдаг. Танил сайтын дараагийн бодлоготой танилцгаая:

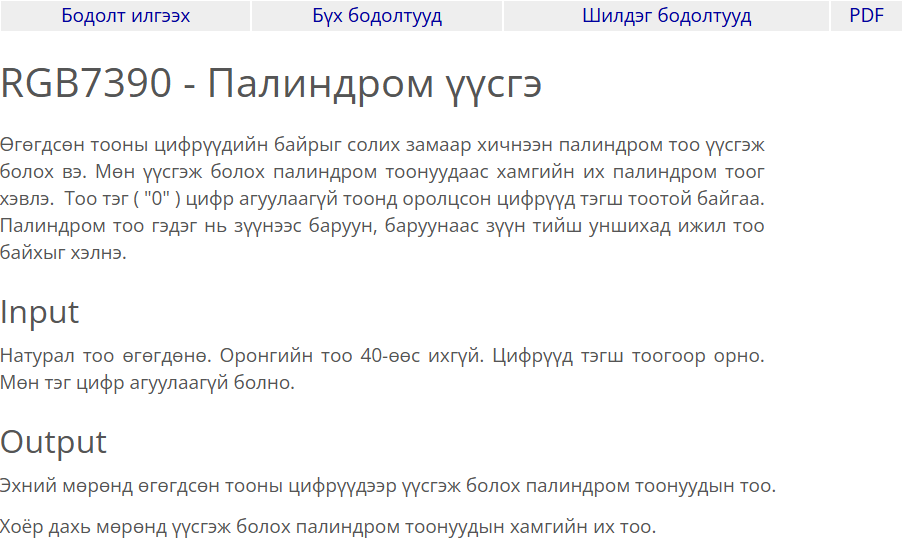
Энэ бодлогын зорилго нь өгөгдсөн натурал тооны цифрүүдийн байрлалыг сольж, хэдэн өөр палиндром үүсгэж болохыг тооцох ба хамгийн их утгатай палиндромыг олох юм.

Палиндром тоо гэж юу вэ?

Палиндром тоо гэдэг нь зүүнээс баруун, баруунаас зүүн тийш уншихад ижил байдаг тоо юм. Жишээ нь:

• 121
• 19891
• 678876
• ….. гэх мэт аль ч талаас нь уншихад ижил тоо байдаг гэсэн үг.

Эндээс бидний ойлгох зүйл бол зүүн тал нь тодорхой бол баруун тал ямар байх нь ойлгомжтой гэдгийг анзаарах юм.

Бодолтоо эхлэхээс өмнө бодлогын жишээ оролт болон үр дүнг харцгаая:

Үр дүнгийн эхний мөрөнд оруулсан тооны хувьд нийт хэдэн палиндром тоо үүсэх боломжтойг, Харин хоёр дахь мөрөнд тухайн үүсэх боломжтой палиндром тоонуудаас хамгийн ихийг нь хэвлэсэн байгаа нь харагдаж байна.

Өгөгдсөн тоонд 0 цифр байхгүй бөгөөд бүх цифр тэгш тоогоор давтагдана хэмээн өгөгдсөн нь палиндром тоо үүсгэх боломжтойг бататгаж байгаа юм.

Алгоритм:

• Оролтын тооны цифрүүдийг тоолох
• 0 цифр болон ямар нэг цифр сондгой тоогоор орсон эсэхийг шалгах
• Палиндром тооны эхний хагасыг үүсгэх
• Хэдэн ялгаатай палиндром тоо үүсэх боломжтойг олох
• Хамгийн их палиндром тоог олох

Эхний алхам: Цифрүүдийг тоолох

Бидний оролтонд орж ирэх тоо тэгш тоо буюу 2-т хуваагдана. Нэг цифр тэгш тоогоор орно. Ингэснээр үүсгэх палиндром тооны эхний хагасад орсон цифр хоёр дахь хагаст адил тоогоор орно гэсэн үг юм.

Жишээ орлтонд 12123333 гэсэн тоо өгөгдсөн. Үүний цифрүүдийг тоолцгооё:

Энд цифрүүдийн тоо:

• 1 цифр 2 удаа
• 2 цифр 2 удаа
• 3 цифр 4 удаа

Үүнийг бүгдээрээ 10 урттай массивт хадгалах хэрэгтэй.

• Индекс нь цифр (0–9)
• Утга нь тухайн цифр хэдэн удаа орсныг хадгална.

Жишээ нь 12123333 тоон дээр:

s = input().strip()
cnt = [0] * 10  # 0–9 цифрийн тоог хадгалах массив

for ch in s:
    cnt[int(ch)] += 1

Алхам 2: Нөхцөл шалгах

0 цифр болон аль нэг цифр сондгой тоогоор орсон эсэхийг шалгах:

if cnt[0] != 0 or any(c % 2 != 0 for c in cnt):
    print(0)
    print()
    exit()

Алхам 3: Палиндром тооны эхний хагасыг үүсгэх

Палиндромын зүүн талын урт = нийт оронгийн тал хувь.
Тиймээс бүх цифрийн тоог 2-т хуваана.

half = [c // 2 for c in cnt]  # Зүүн талын цифрийн тоо
left = "".join(str(d) * half[d] for d in range(9, -1, -1))

Зүүн талд:

• “1” цифр → 1 ширхэг
• “2” цифр → 1 ширхэг
• “3” цифр → 2 ширхэг

Алхам 4: Хэдэн ялгаатай палиндром үүсэх боломжтойг олох

Тайлбар:

• Зүүн талын бүх цифрийн уртыг олж factorial тооцно.
• Давтагдсан цифрүүдийг factorial-ээр хувааж ялгаатай байрлалын тоог олно.

from math import factorial

half_len = sum(half)
ways = factorial(half_len)
for c in half:
    ways //= factorial(c)
print(ways)

Алхам 5: Хамгийн их палиндром тоог олох

1. Зүүн талыг том цифрээс эхлэн үүсгэнэ

Палиндром тоо нь зүүн болон баруун тал хоёр хэсэгт хуваагддаг. Зүүн тал нь эхний хагас цифрүүдийг агуулдаг бөгөөд баруун тал нь үүний толин тусгал шиг урвуу дарааллаар давтагдана.

Иймд хамгийн их утгатай палиндромыг байгуулахын тулд:

right = left[::-1]
palindrome = left + right
print(palindrome)

• Зүүн талын цифрүүдийг томоос жижиг рүү эрэмбэлнэ.
• Тухайлбал, 9 цифрүүдийг эхэлж байрлуулж, дараа нь 8, 7,… гэсэн дарааллаар байрлуулна.

2. Баруун талыг зүүн талын урвуугаар аваад нийлүүлэх

Палиндромын гол чанар нь зүүн тал ба баруун тал нь нэгэн жигд, толь шиг байх.

Тиймээс зүүн талыг үүсгэсны дараа:

• Баруун талд зүүн талын цифрүүдийн урвуу дарааллаар (эхний хэсгийн сүүлийн цифрээс эхлээд) давтсан утгыг тавина.

Жишээ нь:
Зүүн тал: "3321"
Баруун тал: "1233" (зүүн талын урвуу дараалал) Эдгээрийг нийлүүлж бүрэн палиндром үүсгэнэ.

left = "".join(str(d) * half[d] for d in range(9, -1, -1))
right = left[::-1]
result = left + right

Бүтэн код:

from math import factorial

# Оролт авах
s = input().strip()

# Цифр тоолох
cnt = [0] * 10
for ch in s:
    if not ch.isdigit():
        print(0)
        print()
        exit()
    cnt[int(ch)] += 1

# Нөхцөл шалгах
if cnt[0] != 0 or any(c % 2 != 0 for c in cnt):
    print(0)
    print()
    exit()

# Хагас тоо
half = [c // 2 for c in cnt]
half_len = sum(half)

# Ялгаатай палиндромын тоо
ways = factorial(half_len)
for c in half:
    ways //= factorial(c)
print(ways)

# Хамгийн их палиндром
left = "".join(str(d) * half[d] for d in range(9, -1, -1))
right = left[::-1]
print(left + right)

Энэ удаагийн дугаарт бид competitive programming чиглэлд хамгийн түгээмэл орж ирдэг асуудал болох палиндром тоо сэдвийн дунд түвшний бодлогыг Python програмчлалын хэл дээр бодож, асуудлыг шийдлээ.

Уншигч та ямар нэгэн төрлийн бодлогын ард гарч чадъя гэвэл тухайн асуудлыг алгоритмын дагуу буюу зөв, цэгцтэй дарааллаар гүйцэтгэх чадварт суралцаарай. Дараа дараагийн нийтлэлээр уулзталаа түр баяртай. Happy coding!

Боловсролыг Инженерчлэв.

• Facebook
• Instagram