Цуврал нийтлэлээ шимтэн уншдаг та бүхэнтэйгээ дахин уулзахад таатай байна. Бид энэ удаа SPOJ сайтын RGB7 хэсгээс дахин сонирхолтой бодлогыг онцолж, түүнийг хэрхэн үр дүнтэй бөгөөд оновчтой байдлаар бодож болох талаар өгүүлэх болно.
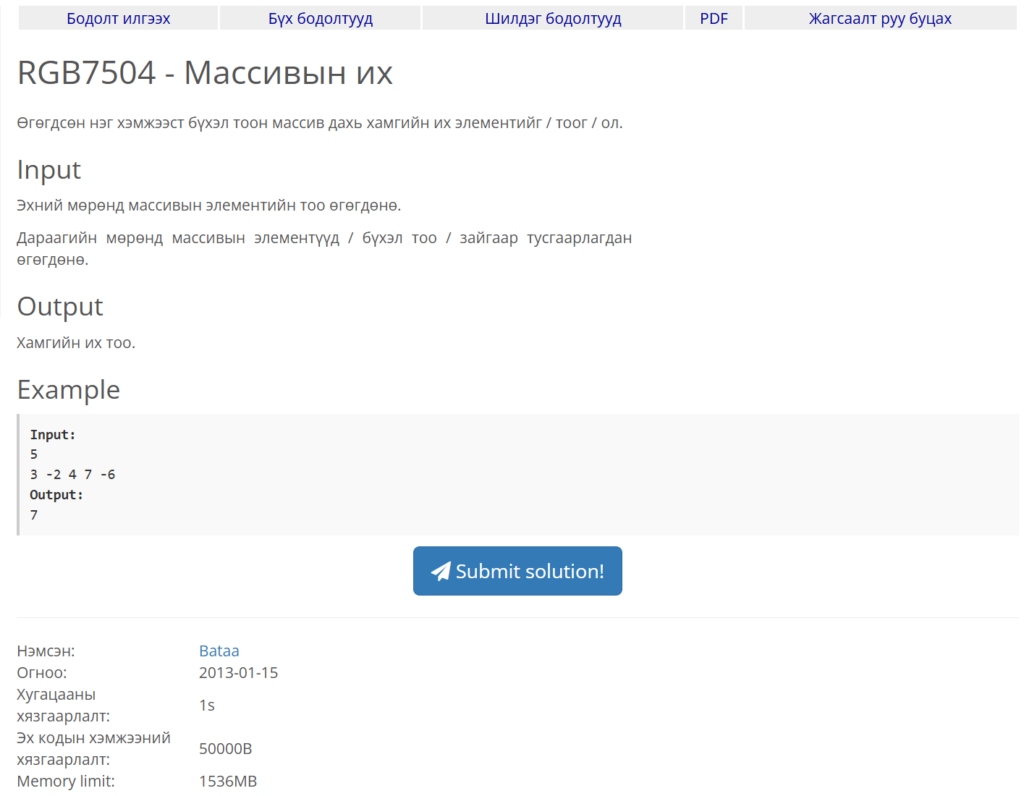
Энэ удаад сонгож авсан бодлого маань уншихад энгийн хэрэгжүүлэлттэй харагдаж байна. Өмнө үзсэнчлэн эхлээд бид бодлогын өгүүлбэрийн сайтар уншиж ойлгох хэрэгтэй. Өгөгдсөн жагсаалт дундаас хамгийн их тоог олох болно.
Жишээлбэл :
Оролт : 7
1 2 3 -2 3 9 -4
Гаралт : 9 буюу хамгийн их тоо.

Хугацаа болон санах ойн хязгаарлалт харгалзан өгөгдсөн ба бүхэл тоон хязгаар өгөгдөөгүй тул бид алгоритмын ажиллах хугацааг урьдчилан тооцоолох боломжгүй байна.
Ингээд бид бодлогын өгүүлбэр болон хязгаарлалтыг уншиж ойлгосон тул өөрсдийн алгоритм аа олох цаг ирлээ. Үүнээс өмнө бид оролтын утгыг хэрхэн зөв авах талаарх мэдлэгээ дахин сэргээж энэхүү нийтлэлээ унших хэрэгтэй. Дараа нь бид алгоритмаа тодорхойлох ба үүнийг хэд хэдэн аргаар олж болно.
Алгоритм -1 : Хамгийн их тоог хайж олох
Жагсаалтаас хамгийн их утгыг олох алгоритм нь хайгуулын нэгэн аялал мэт ажиллана. Алгоритм жагсаалтын эхнээс төгсгөл хүртэл алхам алхмаар явж, бүрэн гүйж дууссаны эцэст хамгийн “хамгийн их” утгыг олж тогтооно. Үүнийг таны өмнө өрөө дүүрэн хайрцаг байгаагаар төсөөлж болно — Та хайрцаг бүрийг нэг нэгээр нь онгойлгож, дотор нь юу байгааг ажиглан, хамгийн томыг нь олох гэж оролдож буй хэрэг. Энэхүү үйл явц нь жагсаалтын хэмжээтэй шууд хамааралтай тул хугацааны хүндрэлийн зэрэг нь O(n) буюу шугаман юм.
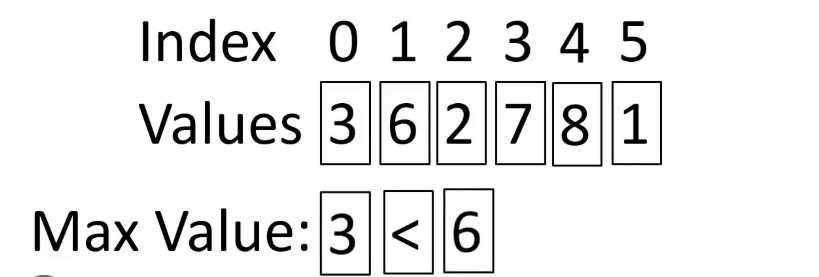
Мэдээж жагсаалтын элементүүд дугаарлалтай байдаг тэр нь 0 ээс эхэлдэг ийг та бүхэн сайн мэдэж байгаа байх. Одоо бидний шийдэх асуудал бол хэрхэн ихийг нь мэдэх вэ ? Бидний сонгож авсан жишээ шиг өрөөнд маш их байгаа харцагануудаа нэг нэгээр нь нээж харахдаа өөрийн цаасан дээр байгаа тэмдэглэсэн хамгийн их утгатай жишээд явахад л болно шүү дээ. Тэгэхээр бид эхлээд хамгийн эхэнд нээх хайрцгаа хамгийн их гэж тэмдэглэх нээ.
# Хэрэглэгчээс жагсаалтын хэмжээ буюу n тоог авна
n = int(input())
# n ширхэг бүхэл тоог нэг мөрөнд оруулж, жагсаалт болгон хадгална
a = list(map(int, input().split()))
# Жагсаалтын эхний элементийг хамгийн их утга гэж онооно
max_value = a[0]
# Жагсаалтын бүх элементээр давталт хийж хамгийн ихийг олно
for i in a:
if i >= max_value:
max_value = i
# Хамгийн их утгыг хэвлэнэ
print(max_value)
Алгоритм – 2 : Жагсаалтыг эрэмбэлэх
Дараагийн арга бол жагсаалтыг эрэмбэлэх. Өөрөөр хэлбэл ангийн сурагчид биеийн тамирын хичээлд орсон байгаа гэж төсөөлье. Бидний даалгавар бол ангийн хамгийн өндөр сурагчийг олох. Өмнөх арга дээр бид хоёр хоёр оор нь зэрэгцүүлээд өндөр хүүхдийг нь үлдээгээд цаашид бүх сурагчийг энэ аргаар хэмжсэн билээ. Одоо бидэнд дахин нэг арга байгаа нь хүүхдүүдийг дэс дарааллаар буюу өндөр намаар нь жагсаах. Тийм ээ ингээд л болоо. Тамирын багш нэг шүгэл үлээгээд л ангийн хамгийн өндөр хүүхэд тодорхой болдог шүү дээ. Python программчлалын хэл дээр жагсаалтыг эрэмбэлэх sort() функц байдаг ба O(n logn) хугацаанд ажилладаг бөгөөд бид үүнийг ашиглан жагсаалтаа эрэмбэлээд хамгийн эхний элементийг авахад л хамгийн их утга олдоно.
# Хэрэглэгчээс жагсаалтын хэмжээ буюу n тоог авна
n = int(input())
# n ширхэг бүхэл тоог нэг мөрөнд оруулж, жагсаалт болгон хадгална
a = list(map(int, input().split()))
# Жагсаалтыг өсөхөөр эрэмбэлнэ
a.sort()
# Эцсийн (хамгийн том) элементийг хэвлэнэ
print(a[-1])
Ингээд бид хамгийн их элемент олох 2 арга мэддэг боллоо. Энэ аргуудыг өшөө дэлгэрүүлэн хамгийн ихийг олох маш олон арга бий. Жишээлбэл Алгоритм – 1 ийг хоёртын хайлтаар хийх. Алгоритм – 2 ийг selection, bubble гэх мэт тухайн бодлогод тохирох эрэмбэлэх аргаар хэрэгжүүлэх зэрэг дурыг аргийг ашиглан хэрэгжүүлж болно. Программчлал бол урлаг хэмээн хэлж байсанчлан уншигчид маань хайрцагт баригдалгүй чөлөөтэй сэтгэх боломжийг Өрсөлдөөнт программчлал маань олгож байгаа билээ. Хэн хамгийн сайн, хурдан аргаар асуудлыг шийднэ, тэр хамгийн мундаг нь . 😎