Энэ удаагийн нийтлэлээр бид SPOJ-ийн RGB7 бодлогыг сонгон авч, нэг төрлийн бодлогыг олон өнцгөөс хэрхэн бодож болох, хугацааны хязгаарлалттай орчинд алгоритм зохиох ур чадварыг хэрхэн хөгжүүлэх талаар судлах болно.
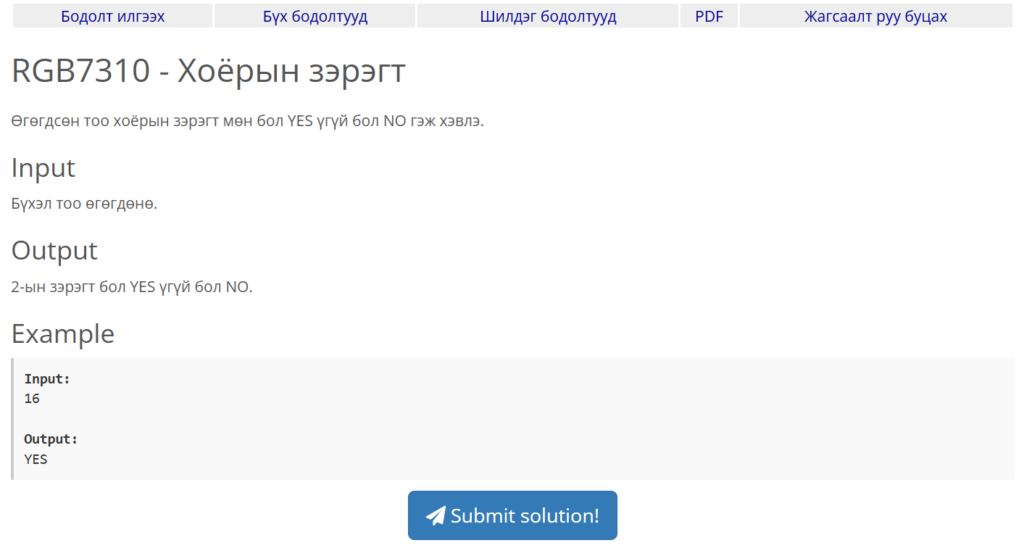
Энэ удаад сонгож авсан бодлого маань ойлгоход хялбар, хэрэгжүүлэхэд энгийн мэт санагдаж болох ч нарийн бодож үзвэл төвөгтэй мэт санагдах болно. Өмнөхийн адил бид эхлээд бодлогын нөхцөлийг сайтар уншиж, юу шаардаж байгааг ойлгох хэрэгтэй. Энэ бодлогын хувьд бидэнд нэг тоо өгөгдөх бөгөөд тухайн тоо хоёрын зэрэгт (2⁰, 2¹, 2², …) мөн эсэхийг шалгах шаардлагатай. Үр дүнд нь “YES” эсвэл “NO” гэж хэвлэнэ.
Жишээлбэл:
Оролт: 8 (Өгөгдсөн тоо: 8)
Гаралт: YES (Учир нь 8 = 2³ )
Хугацаа болон санах ойн хязгаарлалт харгалзан өгөгдсөн ба бүхэл тоон хязгаар өгөгдөөгүй тул бид алгоритмын ажиллах хугацааг урьдчилан тооцоолох боломжгүй байна.
Ингэснээр бид бодлогын өгүүлбэр болон хязгаарлалттай танилцаж, үндсэн нөхцөлийг ойлгож авлаа. Одоо бол алгоритмаа гаргаж, хэрэгжүүлэх цаг ирлээ. Алгоритм боловсруулахдаа нэг л шийдэлд хязгаарлагдалгүй, өөр өөр өнцгөөс хэд хэдэн хувилбараар сэтгэн бодох боломжтой. Бидний сонгож авсан бодлогын хувьд хүснэгтэд харагдах шийдлүүдийг санал болгож байна. (Мэдээж өөр олон янзаар шийдэж болно.)
| АРГА | ДАВУУ ТАЛ | СУЛ ТАЛ |
|---|---|---|
| Давталт (Алг-1) | Энгийн, ойлгомжтой | Том тоонд удаан |
| Битийн шалгалт (Алг-2) | Хамгийн хурдан, бага санах ой хэрэглэнэ | Анхан шатанд төвөгтэй санагдах боломжтой |
| Логарифм (Алг-3) | Ойлгомжтой, математиктай холбогдсон | Floating point алдаа гарч магадгүй |
| Бинар тоон дээр (Алг-4) | Хялбар, ойлгомжтой | Жижиг хэмжээний бит ашиглана |
| Урьдчилсан жагсаалт (Алг-5) | Хурдан хайлт (O(1)) | Санах ой бага зэрэг их хэрэглэнэ |
Алгоритм – 1 : Давталт ашиглах
Энэ аргаар шалгахын тулд бид 1-ээс эхлээд тоог хоёр дахин үржүүлсээр өгөгдсөн тоонд хүрэхийг оролддог. Хэрвээ яг тэнцвэл хоёрын зэрэгт мөн, тэгэхгүй бол биш гэж үзнэ. Энэ нь яг л шатаар нэг нэгээр дээш гарч, тухайн шатанд очих уу, хэтэрчих үү гэдгийг шалгаж байгаа мэт ойлгомжтой арга юм.
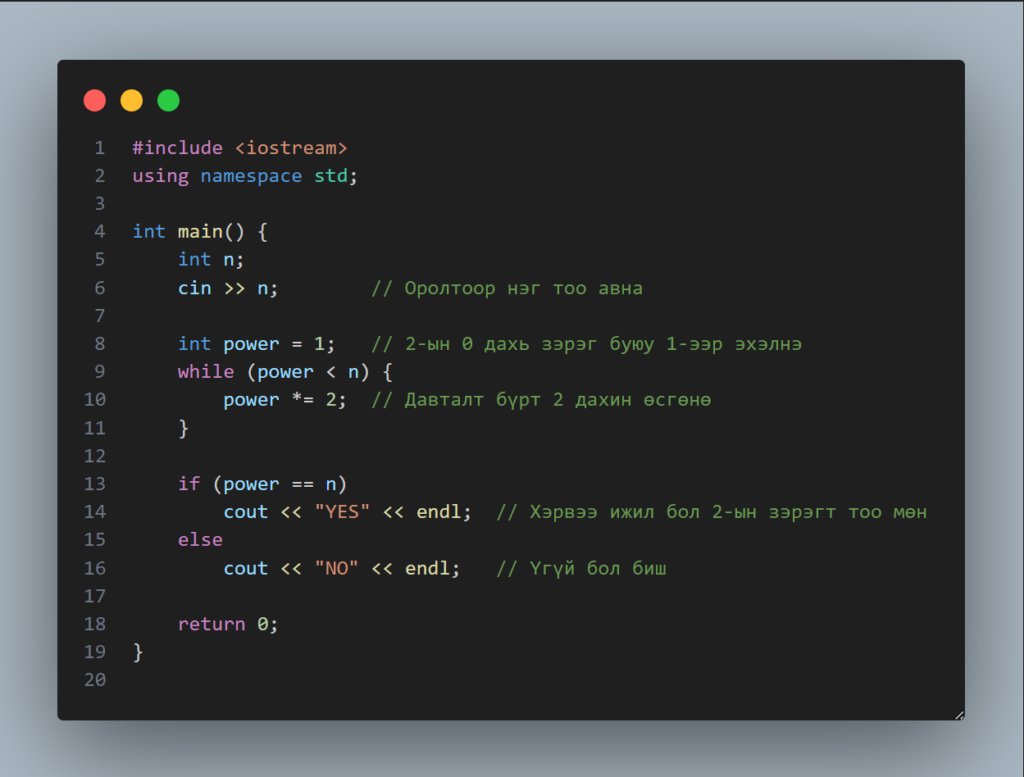
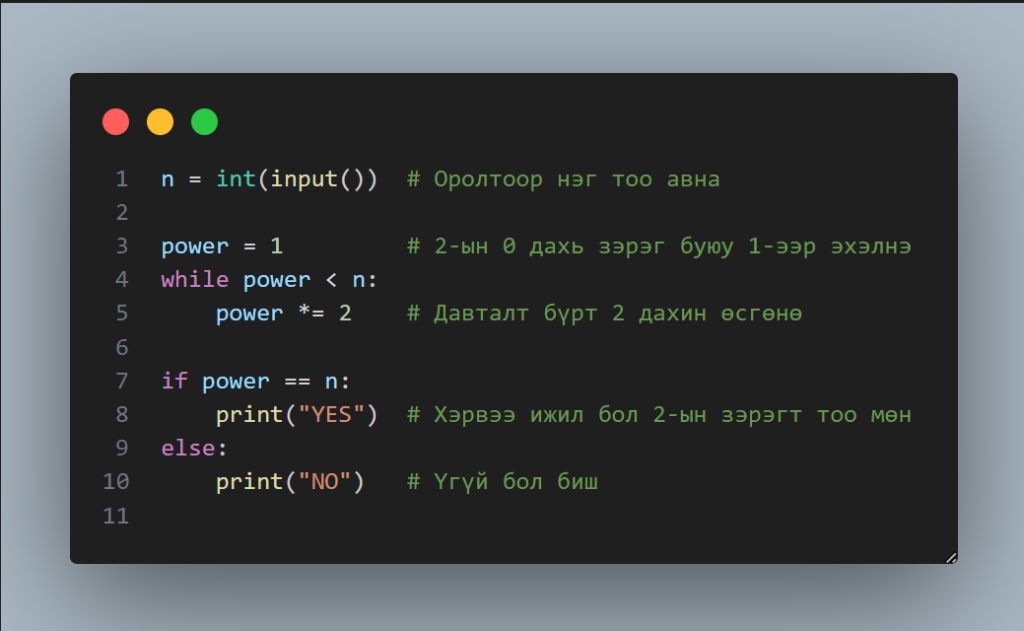
Алгоритм – 2 : Битийн үйлдэл ашиглах арга
Энэ арга нь компьютерийн дотоод бүтэцтэй шууд холбоотой. Хэрвээ тоо нь хоёрын зэрэгт бол түүний хоёртын (битийн) бичлэгт зөвхөн нэг ширхэг “1” ордог. Тиймээс бид n болон n-1 гэсэн хоёр тоог битээр нь харьцуулахад, хэрвээ тэдгээрийн “AND” үйлдэл нь 0 гарвал, тухайн тоо нь хоёрын зэрэгт мөн гэсэн үг. Энэ нь яг л нэг ширхэг гэрэл асаалттай байхад түүний өмнөх бүх гэрэл унтраалттай байгааг шалгаж буй мэт.
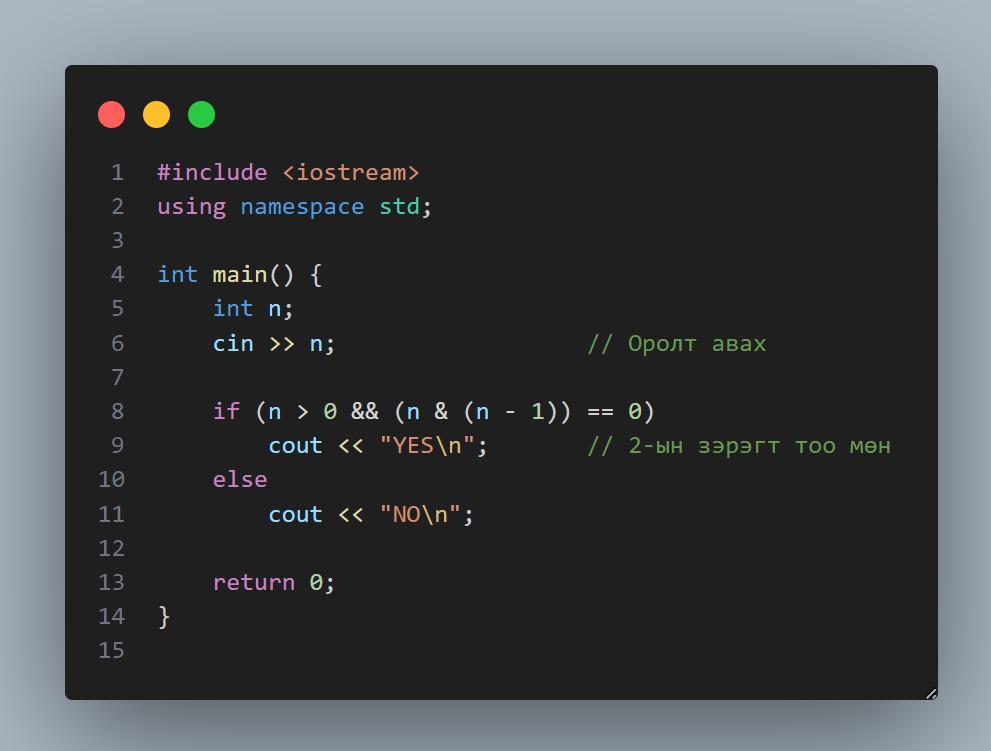
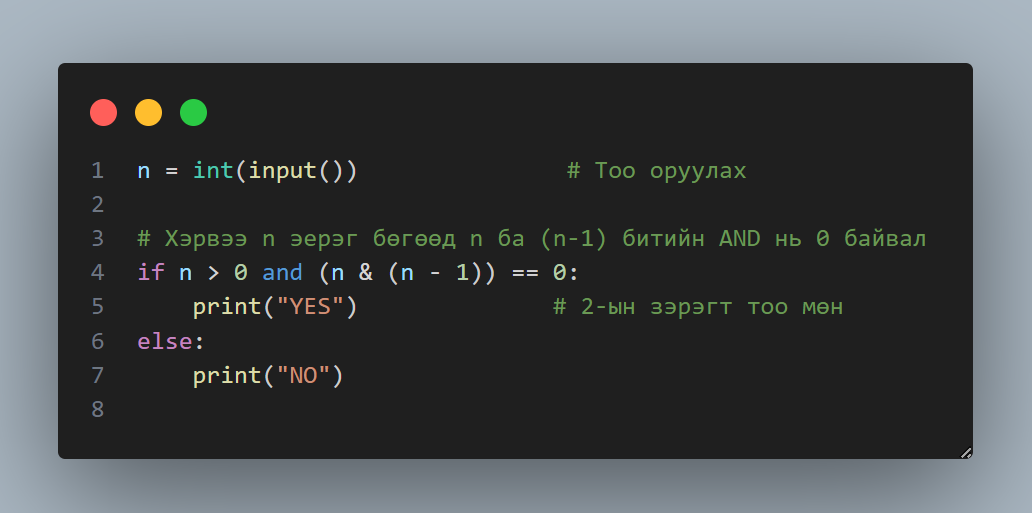
3. Логарифм ашиглах арга
Энэ аргаар шалгахдаа бид тухайн тооны логарифмыг 2 суурьтайгаар авна. Хэрвээ логарифм нь бүхэл тоо гарч ирвэл энэ нь 2-ын хэдэн зэрэгт байгааг илтгэнэ. Тиймээс бүхэл тоо гарвал хоёрын зэрэгт мөн гэж ойлгож болно. Энэ нь яг л “энэ тоо нь 2-ыг хэдэн удаа үржүүлээд гарсан үр дүн вэ?” гэдгийг математикаар асууж байгаа хэрэг юм.
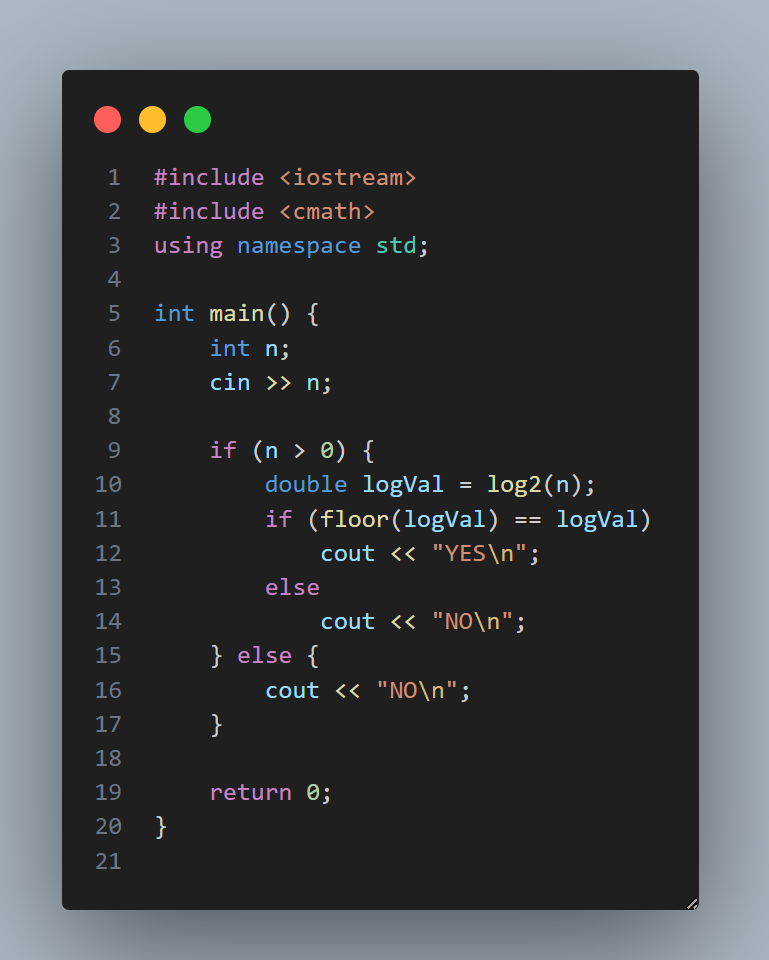
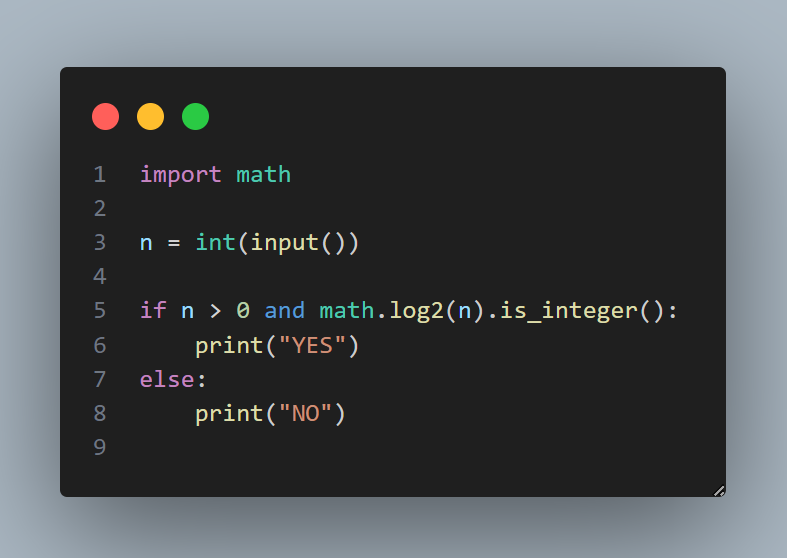
4. Хоёртын (бинар) бичлэгт анализ хийх арга
Бид тухайн тоог хоёртын хэлбэрт хөрвүүлж, хэдэн ширхэг “1” орсон байгааг тоолдог. Хэрвээ яг нэг ширхэг “1” байвал хоёрын зэрэгт мөн гэж үзнэ. Энэ нь яг л тооны дотоод бүтцийг нээж харж, “энэ тоо нэг л гол хүчтэй элементтэй байна уу?” гэж шалгаж буй мэт.
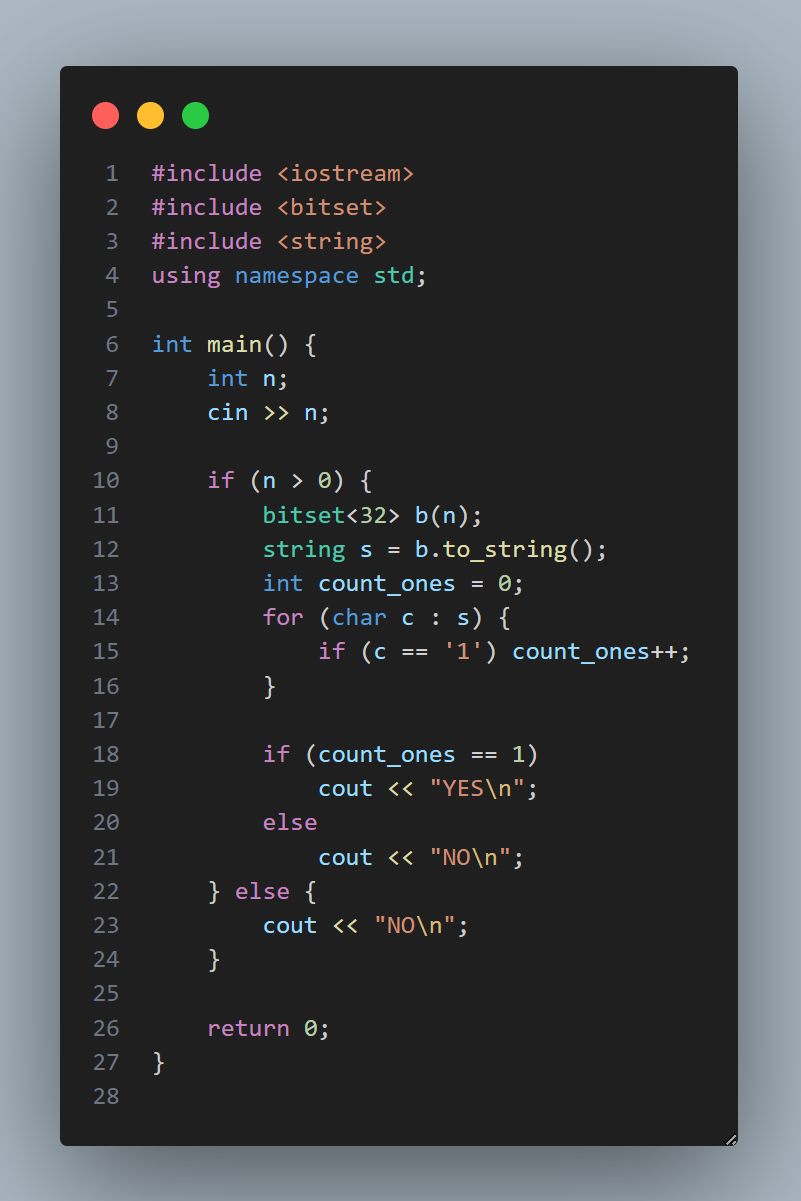
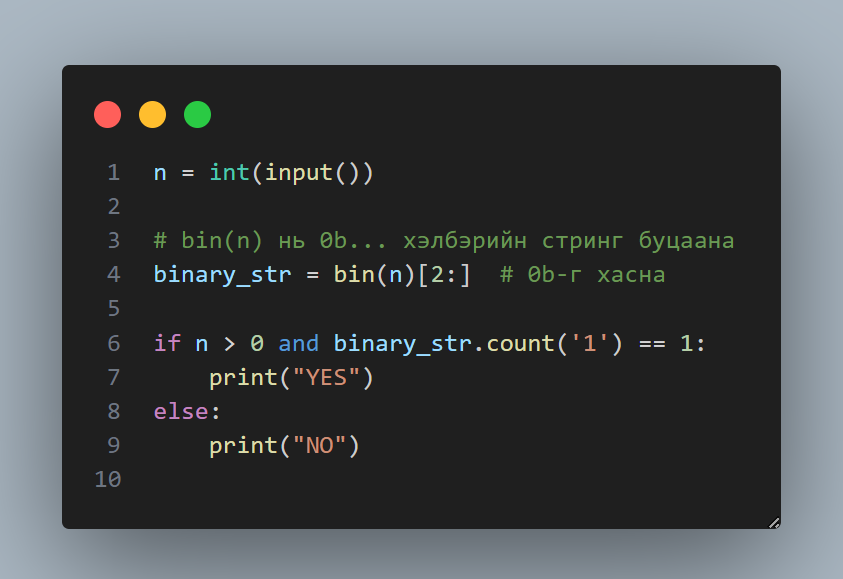
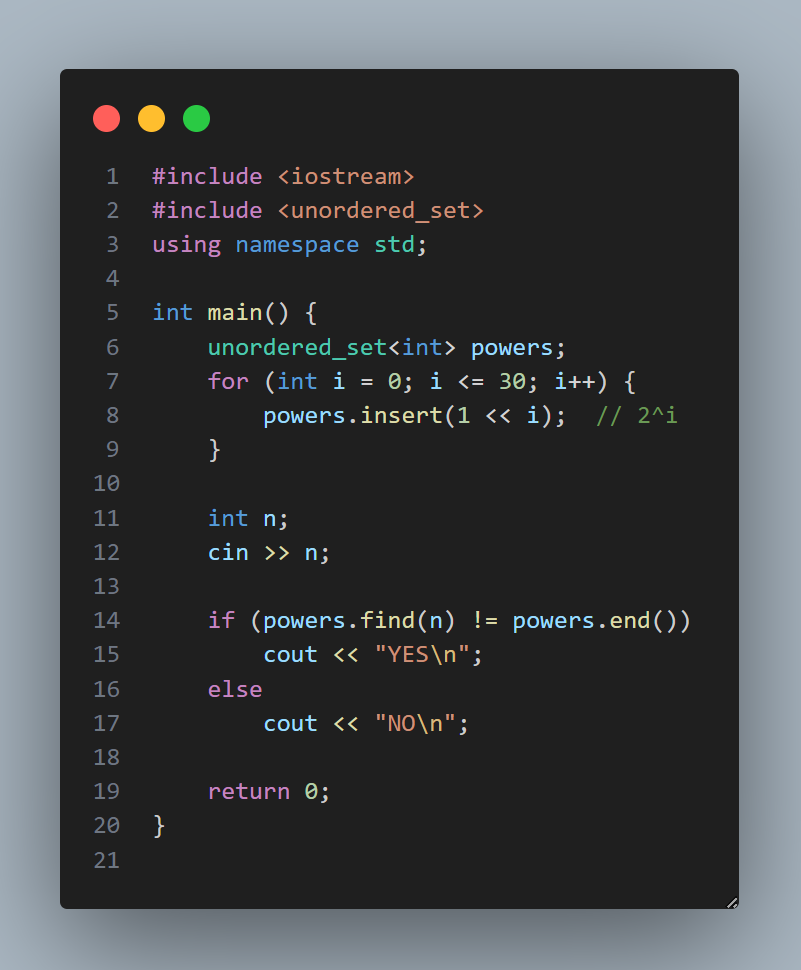
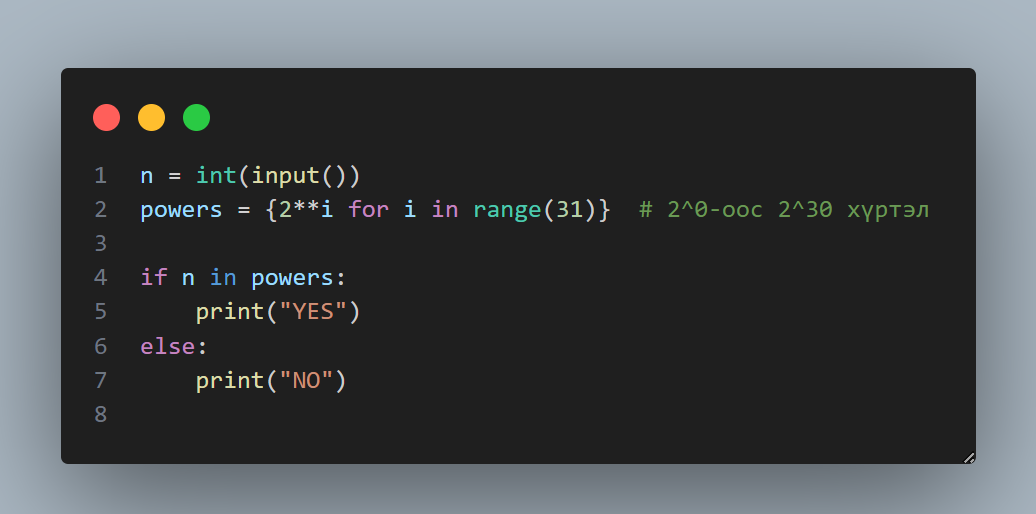
5. Бэлтгэгдсэн жагсаалт ашиглах арга
Энэ аргаар бид эхэндээ бүх хоёрын зэрэгт тоонуудыг урьдчилан жагсааж хадгална (жишээ нь: 1, 2, 4, 8, 16, 32, …). Дараа нь шалгах тоо энэ жагсаалтанд байгаа эсэхийг шалгаж “тийм” эсвэл “үгүй” гэж хэлдэг. Энэ нь яг л тусгай бүртгэлтэй жагсаалт руу хараад “энэ хүн нэр дээр байгаа юу?” гэж шалгаж буйтай ижил.
Өнөөдөр бид нэг бодлогыг хэрхэн олон янзаар шийдэж болох талаар үзлээ. Цаашид илүү сонирхолтой арга шийдлүүдийг оруулах болно.
Өрсөлдөөнт программчлал бидэнд зөвхөн техник мэдлэг бус, асуудалд хэрхэн бүтээлчээр хандахыг сургадгаараа үнэ цэнтэй. Хэн хамгийн хурдан, цэвэрхэн, оновчтой алгоритмаар асуудлыг шийднэ — тэр л хамгийн мундаг нь!
Шинэ бичвэрүүд
Lo-Fi vs Debugging 2025-06-19
DFS vs BFS: Гүн чухал уу? Өр 2025-06-18
