Магадлалт үндэслэл дэх Байесын сүлжээ

Биндэрцэцэг Цэдэн-Иш

• 2025-10-19
• artificial intelligence, graph, network, probabilistic reasoning, probability, граф, магадлал, магадлалт шийдвэр гаргалт, Сүлжээ, хиймэл оюун

“Шүүмжлэлт сэтгэлгээ бол идэвхтэй бөгөөд тасралтгүй үйл явц юм. Энэ нь бид бүгдээрээ Байесчууд шиг сэтгэж, шинэ мэдээлэл ирэх тутамд мэдлэгээ шинэчлэхийг шаарддаг.”

— Даниел Левитин

Магадлалт үндэслэл

Магадлалт үндэслэл нь тодорхойгүй байдлыг илэрхийлэх, шинжлэх үр дүнтэй арга хэрэгсэлд тулгуурладаг. Магадлалын онолын зарчмуудад үндэслэсэн энэ нь бүрэн бус мэдээллийн дор байж болзошгүй үр дүнг гаргах, үйл явдлыг урьдчилан таамаглах, шийдвэр гаргах бүтэцтэй аргуудыг санал болгодог эл тогтолцоо дотроос Байесын сүлжээ нь магадлалт хамаарал бүхий цогц системийг загварчлах чамин бөгөөд хүчирхэг арга гэдгээрээ ялгардаг. Математикч Томас Байесын нэрээр нэрлэгдсэн эдгээр сүлжээнүүд нь графын онолыг ашиглан хамтын тархалтыг хялбарчилж, хиймэл оюун ухаан, эрүүл мэнд, шийдвэрийн шинжилгээ зэрэг салбарт зайлшгүй шаардлагатай болгодог.

Байесын зарчим

Нөхцөлт нягт дахь хувьсагчдыг бас нөхцөлт магадлал дахь үзэгдлүүдийг жинхэнэ уялдаа холбооных нь эсрэг чиглэлээс авч үзэх өөрөөр хэлбэл X хувьсагч Y хувьсагчаас, A үзэгдэл B үзэгдлээс хамаардаг байтал f_{Y | X} (y | x) нөхцөлт нягт, P(B | A) нөхцөлт магадлал шаардлагатай болох явдал тохиолддог. Ийм үед эдгээрийн байрыг соливол бодлого хөнгөрнө. Ийнхүү байр солих буюу холбоо хамаарлыг жинхэнэ уялдаа холбооных нь зүгээс судлах боломжийг Байесын томьёо олгодог. Холбоо хамаарлыг үүн шиг нөгөө талаас нь авч үзэхийг Байесын зарчим харин уг зарчимд тулгуурласан статистик шинжилгээг Байесын шинжилгээ гэдэг.

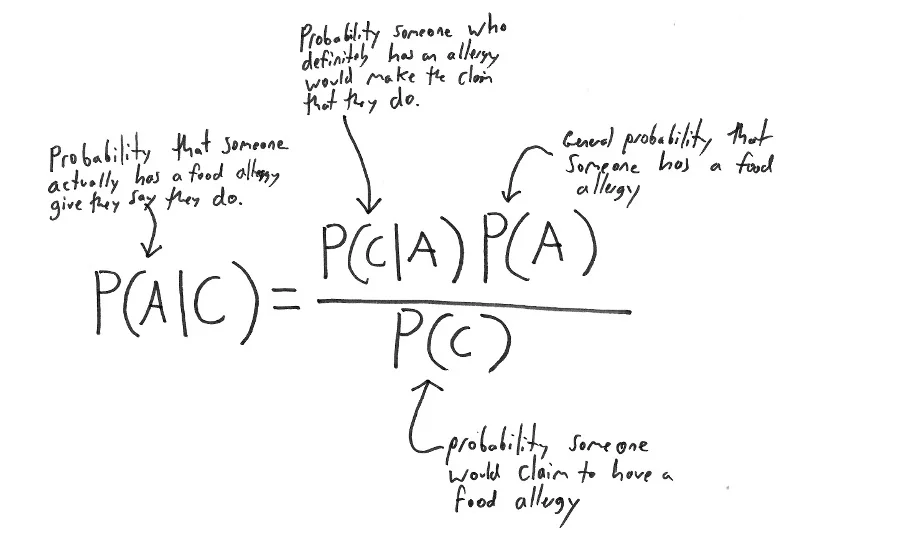
Байесын сүлжээний бүтэц

Байесын сүлжээ нь чиглэлтэй, циклгүй граф бөгөөд үүнд:

• Оройнууд нь дискрет эсвэл тасралтгүй байж болох санамсаргүй хувьсагчийг төлөөлдөг;
• Ирмэгүүд нь хувьсагчдын хоорондын шууд магадлалт хамаарлыг илэрхийлдэг;
• Орой тус бүр P( X_i | Parents( X_i )) нөхцөлт магадлалын хүснэгтүүдтэй нь түүний төлөв байдалд эцэг хувьсагчийн нөлөөллийг тодорхойлдог.

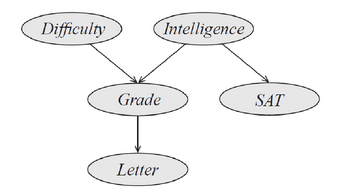
Чиглэлтэй ирмэгүүд нь эцэг, хүүхдийн хамаарлыг бий болгож, орой бүрийн магадлалд түүний өвөг дээдэс хэрхэн нөлөөлж байгааг тодорхойлдог. Хамгийн чухал нь хоёр оройн хооронд ирмэг байхгүй байх нь тодорхой нөхцөлд нөхцөлт үл хамаарлыг илтгэж, магадлалын тооцооллын нарийн төвөгтэй байдлыг эрс багасгадаг.

Нөхцөлт үл хамаарал

Байесын сүлжээний гол онцлогуудын нэг бол нөхцөлт үл хамаарал ашиглах чадвар юм. Энэ шинж чанар нь хувьсагчдын хамтын тархалтыг жижиг, удирдах боломжтой бүрэлдэхүүн хэсгүүдэд оруулах боломжийг олгодог. X₁ , X₂ , . . . , X_n хувьсагчдыг Байесын сүлжээгээр төлөөлүүлсэн тохиолдолд хамтын магадлалыг дараах байдлаар илэрхийлж болно.

Байесын сүлжээний сонгодог жишээ бол дүнгийн сүлжээ (Student Model) бөгөөд дараах хувьсагчдын хоорондын хамаарлыг загварчилдаг. X_i оройны эцэг орой нь X_i -д шууд нөлөөлдөг бүх эцэг X₁ , X₂ , . . . , X_i-1  оройнуудыг агуулсан байх ёстой. Энэ сүлжээнд:

• Difficulty (d): Хичээл хүнд, хөнгөн эсэх;
• Intelligence (i): Оюутны оюуны чадамж сайн, муу эсэх;
• Grade (g): Хичээлийн дүн сайн, дунд, муу эсэх;
• SAT (s): SAT шалгалтын оноо сайн, муу эсэх;
• Letter (l): Багшийн тодорхойлолт дээр сайн, муу байсан эсэх орно.

Grade-д Difficulty эсвэл Intelligence байгаа эсэх нь мэдээж нөлөөлсөн боловч шууд нөлөөлөөгүй. Grade-ийг харгалзан үзвэл, Letter нь SAT-д ямар ч нөлөө үзүүлэхгүй. Иймд Grade нь Letter-ийн цорын ганц эцэг болох буюу P(Letter | SAT, Grade, Intelligence, Difficulty) = P(Letter | Grade) байна. Учир нь орой бүр нь зөвхөн өмнөх оройтой холбогдсон байх тул уг граф нь циклгүй. Байесын сүлжээнүүдийн өөр нэг чухал шинж чанар нь тэдгээр нь илүүдэл магадлалын утгыг агуулаагүй явдал юм. Хэрэв илүүдэл байхгүй бол үл нийцэх боломж үүсэхгүй.

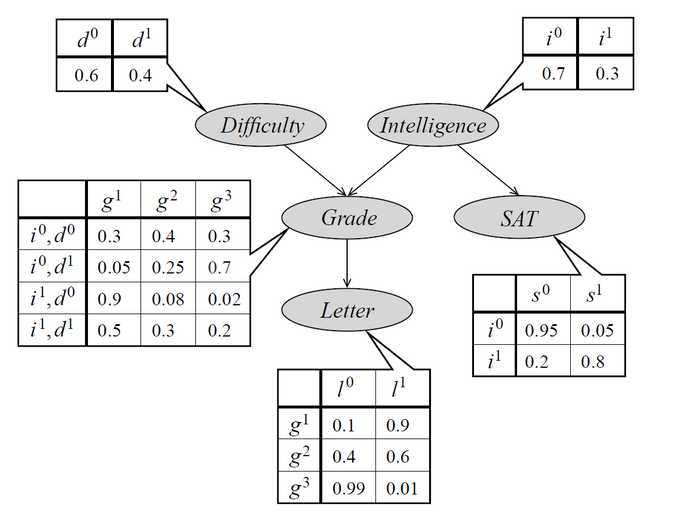
Дүгнээд хэлбэл, магадлалт үндэслэл нь тодорхой бус нөхцөлд мэдлэгээ шинэчилж, шийдвэр гаргах хамгийн зохион байгуулалттай арга замуудын нэг юм. Байесын зарчим нь нөхцөлт магадлалын харилцааг хоёр чиглэлд авч үзэх боломж олгож, мэдээллийг шинээр ирэх бүрт уян хатан байдлаар үнэлэх онолын суурийг бүрдүүлдэг. Үүний бодит хэрэгжилт болох Байесын сүлжээ нь графын онол, статистикийн уялдаа холбоог нэгтгэн, цогц системүүдийн дотоод хамаарлыг ил тод, тооцооллын хувьд үр ашигтай хэлбэрээр загварчлах хүчирхэг арга юм.

Нөхцөлт үл хамаарлын зарчимд тулгуурласан эдгээр сүлжээ нь олон хувьсагчдын хамтын тархалтыг удирдах боломжийг олгож, мэдээлэлд суурилсан шийдвэр гаргалт, урьдчилан таамаглал, хиймэл оюун ухааны загварчлал зэрэг орчин үеийн шинжлэх ухааны үндсэн хэрэглүүрийн нэг болж байна. Иймд Байесын тогтолцоо нь магадлалын онолыг практикт хэрэглэх хамгийн ухаалаг, тасралтгүй хөгжиж буй хандлагуудын нэг гэж үзэж болно.